Observation et présentation
Nous allons calculer la masse de Jupiter à partir de l'observation de ses satellites grâce à un télescope.
Présentation
Pour réaliser les observations de Jupiter et de ses quatre satellites principaux, on utilise un simulateur qui nous replace dans les mêmes conditions d'observation que si elles étaient réalisées au télescope.
Le simulateur représente ce que l'on voit à travers l'occulaire du télescope: on peut donc observer le défilement des satellites devant la planète. Ce défilement est du au mouvement de rotation de la Terre sur elle-même.
L'occulaire de ce télescope est du type réticulé: c'est à dire qu'il est composé d'une croisée de fils qui restent immobiles dans le champ d'observation. Ils nous permettent donc de mesurer la distance apparente entre le centre de la planète et celui de chacun de ses satellites.
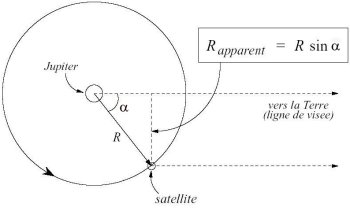
En effet, les différentes lunes apparaissent alignées car leur orbite est vue par la tranche, mais les satellites bougent par rapport à Jupiter au bout d'un ceratin temps: on ne voit de la Terre que la projection de ce mouvement dans le plan du ciel. La distance que l'on observe est dons la distance apparente, c'est à dire la distance entre le satellite et la droite joignant Jupiter à la Terre (la ligne de visée).
La distance réelle est donnée par la relation :
D = Dapp/sin alpha
D = distance réelle
Dapp = distance apparente
alpha = angle entre la ligne de visée et la distance réelle Jupiter/satellite
Pour réaliser nos mesures, la distance apparente est suffisante: elle est donnée en seconde et est mesurée grâce au chronomètre dont est équipé le télescope.
On trouve aussi sur le simulateur la raquette du télescope: c'est elle qui permet de commander les moteurs du télescope s'il y en a. Ils aident à diriger celui-ci: le redresser, le baisser ou le diriger sur les côtés. Ici, on peut utiliser la raquette pour recentrer les satellites ou la planète.
Résultats
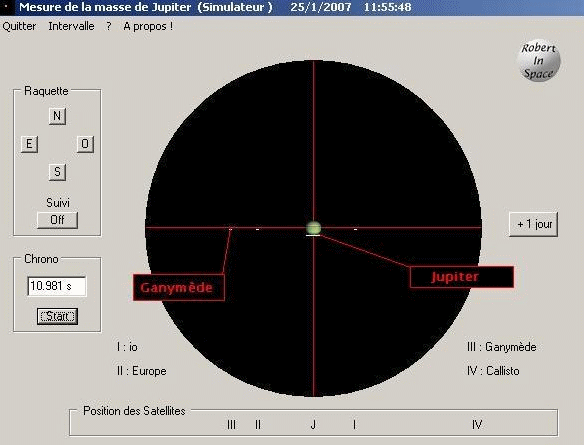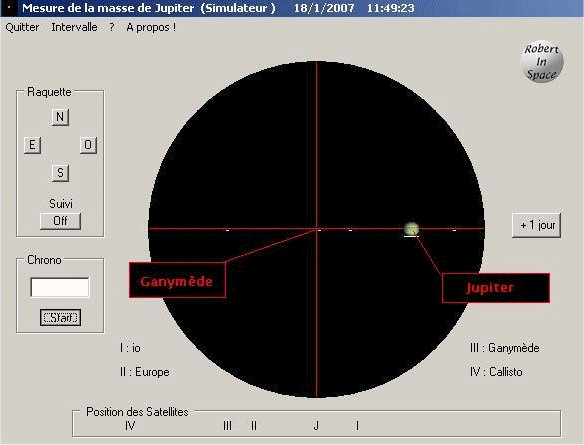
On réalise l'observation d'un satellite chaque jour pendant cinq jours: un seul satellite est nécessaire pour les calculs: on a donc observé Ganymède (tout à fait arbitrairement). On réalise l'opération plusieurs fois pour chaque jour: cela permet de faire une moyenne de nos mesures et de vérifier qu'aucune d'elle n'est improbable. (capture d'écran)
On a réalisé deux séries de mesures à des dates différentes afin de pouvoir utiliser deux méthodes différentes dans la suite du calcul.
Voici les résultats obtenus pour l'observation de Ganymède:
| Date | Temps de défilement |
| 07-déc | -22,00s |
| 08-déc | -4,8s |
| 09-déc | 15,8s |
| 10-déc | Mauvais temps: pas d'observation possible |
| 11-déc | 20,04s |
| 12-déc | 6,6s |
------------
| Date | Temps de défilement |
| 20-fév | 19s |
| 21-fév | 5s |
| 22-fév | -12s |
| 23-fév | -21s |
| 24-fév | -13s |
| 25-fév | 4s |
| 26-fév | 19s |
| 27-fév | 21s |
| 28-fév | 8s |
| 1-mars | -10s |
| 2-mars | -20s |
| 3-mars | -15s |
Lorsque le satellite se situe à l'ouest de Jupiter, on met un signe "-" devant les mesures.
Le temps de défilement correspond à la distance apparente entre le satellite et le planète: on a donc les différentes distances sur plusieurs jours; on va ainsi pouvoir calculer la période révolution de Ganymède. Pour la suite du calcul, on aura besoin du diamètre apparent de Jupiter:on va donc utilisr le simulateur pour obtenir cette donnée. Par la même méthode que précédemment, on mesure la distance entre les deux extrémités de Jupiter. On obtient: diamètre apparent de Jupiter = 3s.