Période de révolution et demi-grand axe
Période de révolution de Ganymède
Calcul du demi-grand axe
La période de révolution de Ganymède
Maintenant que l'on a les différentes distances entre le satellite et la planète, nous allons pouvoir calculer la période de révolution de Ganymède.
Méthode 1
Pour cela, on va d'abord utiliser une méthode graphique.
D'après la première loi de Kepler, l'orbite des satellites de Jupiter est normalement elliptique. Une ellipse est définie comme la section d'un cône par un plan. Mais pour simplifier les calculs, on prendra une orbite circulaire. En effet, la trajectoire des satellites autour de Jupiter est très proche du cercle: nos résultats ne seront donc pas modifiés.
Pour tracer le graphique, on peut utiliser du papier milimètré, ou bien le logiciel Geogebra.
Sur l'axe des abscisses, on place le point où la distance apparente a été la plus grande:elle est notée Tmax et a eu lieu le 7 décembre. Le centre de l'axe des abscisses est Jupiter ( noté J ). A paritr de là, on définit une échelle: le point Tmax correspond à une distance apparente de -22s; il a été positionné à -7 unités. On utilise les produits en croix pour placer les distances apprentes aux autres dates. Par exemple, le point 8 se trouve à : -4,8*7/22 = -1,5.
Sous cet axe, on dessine un cercle de centre J et de rayon Tmax: c'est la reconstitution de l'orbite de Ganymède. On reporte sur le cercle les mesures qu'on a relevées grâce au télescope par projection verticale: cela nous donne les différentes positions du satellite au cours du temps.
On trace ensuite la droite reliant le point de la première observation à Jupiter, puis celle allant du point de la dernière observation à Jupiter. On obtient un angle qui correspond à la portion d'orbite parcourue par le satellite pendant les jours d'observation.
Dans notre exemple, le satellite a parcouru un angle de 252° et notre observation a duré 5 jours. Soit un angle de 252/5 = 50,4° par jour.
L'orbite étant circulaire, le satellite parcourt 360° lors de sa révolution et on a vu que le satellite parcourt un angle de 50,4° par jour, donc on calcule sa période en divisant l'angle parcourut au total par l'angle parcouru en un jour: 360/50,4 = 7,14
Le satellite a une période de révolution de 7,14 jours (la valeur officielle de la période de révolution de Ganymède est, d'après les Ephémérides Astronomiques, de 7,155 jours.
Méthode 2
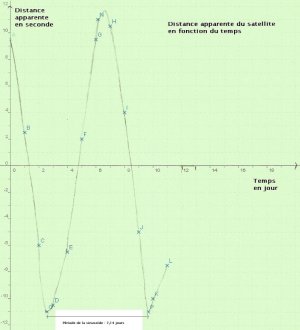
Il existe une deuxième méthode pour calculer la période de révolution : il suffit de tracer la courbe représentant la distance apparente en fonction du temps.
La courbe obtenue est une sinusoïde. La période de cette courbe est de 7,14 jours. On en conclue donc que la période de révolution de Ganymède est de 7,14 jours.
Calcul du demi-grand axe
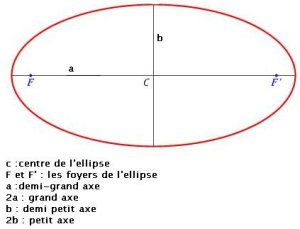
Une ellipse est définie comme le lieu des points dont la somme des distances à deux points fixes (appelés les foyers de l'ellipse) est une constante . Elle comporte deux axes. L'axe le plus long est appelé le grand axe de l'ellipse.
On calcule ici le demi-grand axe, c'est à dire la moitié de la mesure du grand axe. Puisque l'on considère que la trajectoire de Ganymède est circulaire, le demi-grand axe correspond en réalité au rayon du cercle formé par cette trajectoire, et dont le centre est Jupiter.
Pour le calculer, on va utiliser une simple règle de trois. Grâce au simulateur, on a calculé le diamètre apparent de Jupiter: c'est à dire quel était le temps de défilement de Jupiter dans l'occulaire. On a trouvé 3s.
Le diamètre officiel de Jupiter est de 124 743 km . On peut donc trouver à combien de km correspond une seconde observée dans le simulateur. 124743/3 = 47581. Donc une seconde correspond à 47 581 km.
L'élongation maximum était de 22 s. Le demi-grand axe est donc de: 47 581*22 = 1 046 782 km.